เครื่องมือคำนวณปริมาตรรูปวงรี

ต้องยอมรับว่า—คำว่า "รูปวงรี" ไม่ใช่คำที่เราใช้ในชีวิตประจำวันบ่อยๆ แต่คุณอาจประหลาดใจที่ว่า รูปวงรี นั้นอยู่รอบตัวเราแทบทุกที่ เคยถือไข่ขณะอุ้ม หรือลูกบอลรักบี้ หรือเคยเห็นโลกจากอวกาศไหม? คุณได้สัมผัสกับรูปวงรีอย่างแน่นอน สำหรับรูปร่างสามมิติทุกรูปแบบ—จากทรงกรวยถึงพีระมิด—คุณจะพบเครื่องมือทั้งหมดได้ที่ หน้าคำนวณปริมาตรหลัก

รูปวงรีคืออะไร?

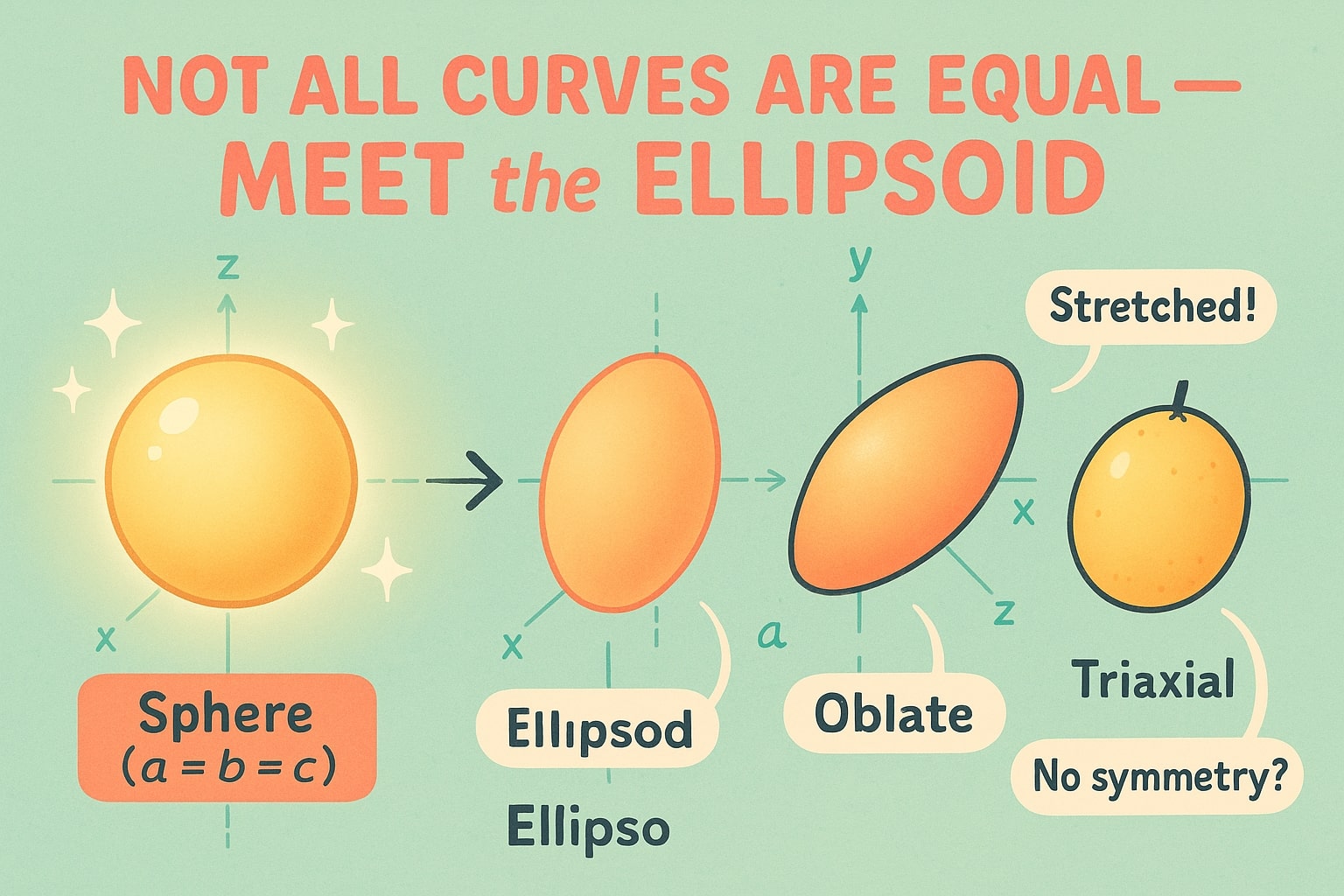
เริ่มต้นจาก ทรงกลม—วัตถุสามมิติที่กลมสมบูรณ์แบบ เช่นเดียวกับการนึกภาพว่าคุณกดให้มันแบนลงเล็กน้อยหรือยืดออกทางด้านข้าง รูปร่างโค้งมนที่ไม่เท่ากันในทุกทิศทางนี้คือ รูปวงรี

ในทางเรขาคณิต รูปวงรี อธิบายโดยการใช้แกนสามแกน:

• a = ความยาวตามแกน x

• b = ความยาวตามแกน y

• c = ความยาวตามแกน z

ถ้า a b และ c เท่ากันหมด แสดงว่าคุณกำลังดู ทรงกลม แต่ถ้าต่างกันแปลว่าอยู่ในกลุ่ม รูปวงรี

รูปวงรีมีหลายแบบที่พบบ่อย:

• รูปวงรีโปรเลต : ยืดออกตามแกนหนึ่ง (เหมือนลูกบอลรักบี้)

• รูปวงรีโอเบลต : ถูกกดทับตามแกนหนึ่ง (เหมือนโลกของเรา!)

• รูปวงรีแทรกซ์เชียล : แกนทั้งสามแตกต่างกันทั้งหมด (ไม่มีสมมาตร—นึกถึงผลไม้ทรงแปลกหรือแคปซูลยา)

ตั้งแต่รูปร่างของดาวเคราะห์ เซลล์ ไปจนถึงไข่ปลา รูปวงรี พบเห็นบ่อยกว่าที่คิด นั่นเป็นเหตุผลว่าทำไมการรู้วิธีคำนวณ ปริมาตร จึงเป็นประโยชน์มาก

เมื่อคุณคำนวณปริมาตรได้แล้ว คุณยังสามารถแปลงปริมาตรเป็นลิตร แกลลอน หรือหน่วยอื่นๆ ได้อย่างรวดเร็วด้วย เครื่องมือแปลงปริมาตร

วิธีคำนวณปริมาตรรูปวงรี

ข่าวดีคือ สูตรคำนวณ ปริมาตร นั้นง่ายมาก ถ้าคุณรู้ความยาวของแกนกึ่งกลางสามแกน (กึ่งแกน คือครึ่งหนึ่งของเส้นผ่านศูนย์กลาง) ได้แก่ a b และ c ก็ใช้สูตรนี้ได้เลย:

ปริมาตร = (4/3) × π × a × b × c

แค่นี้เอง คุณแค่คูณความยาวกึ่งแกนทั้งสามเข้าด้วยกัน แล้วคูณด้วยค่าไพ (π) และคูณด้วยสัดส่วนสี่ในสาม

หมายเหตุสำคัญ: ตรวจสอบให้แน่ใจว่าคุณใช้ความยาวกึ่งแกน ไม่ใช่เส้นผ่านศูนย์กลางเต็มตัว ถ้ารูปวงรีของคุณกว้าง 10 ซม. คุณควรใช้ 5 ซม. ในสูตร

สมมติว่ารูปวงรีของคุณมีความยาวกึ่งแกน 4 ซม. 3 ซม. และ 2 ซม.
คุณจะคำนวณปริมาตรได้แบบนี้:

ปริมาตร = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100.53 ซม.³

ถ้ากึ่งแกนทั้งสามเท่ากัน เช่น 5 ซม. ทุกแกน รูปวงรีนี้เป็นทรงกลมจริงๆ ในกรณีนี้สูตรจะกลายเป็นสูตรทรงกลมคลาสสิก:

ปริมาตร = (4/3) × π × r³

💡 คำแนะนำพิเศษ: ถ้ารูปร่างของคุณคล้ายทรงกลมแล้ว คุณสามารถประมาณปริมาตรโดยใช้สูตรทรงกลม หรือง่ายกว่านั้นคือใช้ เครื่องมือคำนวณปริมาตรทรงกลม

เกาส์และรูปร่างของโลก

ย้อนกลับไปในต้นศตวรรษที่ 19 ก่อนจะมีดาวเทียมหรือ Google Earth นักคณิตศาสตร์ชาวเยอรมันที่ชื่อ คาร์ล ฟริดริช เกาส์ ได้ตั้งคำถามที่กล้าหาญว่า: โลกมีรูปร่างอย่างไรจริงๆ?

หลายคนคิดว่าโลกเป็น ทรงกลมสมบูรณ์ แต่เกาส์สงสัย เขาคาดว่าโลกถูกกดทับเล็กน้อยที่ขั้วโลก ซึ่งเราเรียกว่า รูปวงรีโอเบลต แทนที่จะอยู่แค่ในทฤษฎี เขาลงพื้นที่จริง ปีนเขา ขนเครื่องมือ และพัฒนาวิธีวัดระยะทางยาวๆ ด้วยความแม่นยำสูงสุด

ความพยายามที่บุกเบิกของเขาช่วยสร้างศาสตร์ที่เรียกว่า จีโอดีซีย์ ซึ่งศึกษารูปร่างและขนาดของโลก และเขาก็ถูกต้อง: โลกไม่กลมสมบูรณ์ มันนูนที่เส้นศูนย์สูตรและแบนที่ขั้วโลก—ข้อมูลสำคัญสำหรับการออกแบบระบบดาวเทียมและการคำนวณพิกัดทั่วโลกอย่างแม่นยำ

ข้อเท็จจริงน่าสนใจเกี่ยวกับรูปวงรี

• โลกไม่ใช่ทรงกลมสมบูรณ์—แต่เป็น รูปวงรีโอเบลต หมายความว่ามีขนาดกว้างกว่าที่เส้นศูนย์สูตร ความแตกต่างนี้มีแค่ไม่กี่มิลลิเมตรแต่สำคัญต่อ GPS และการนำทางในอวกาศ
• ไข่เป็นรูปวงรีตามธรรมชาติ แม้ไม่สมบูรณ์แต่ไข่ไก่มีรูปทรงที่คล้ายรูปวงรีมากจนถึงขั้นนักวิทยาศาสตร์ใช้ สูตรวงรี ในการประมาณปริมาตรเพื่อการวิจัยทางการเกษตร
• ก้อนหินอวกาศและดวงจันทร์หลายดวงมีรูปร่างเหมือนรูปวงรี ไม่ใช่ทรงกลม เพราะแรงโน้มถ่วงของมันไม่แรงพอจะดึงให้เป็นทรงกลมสมบูรณ์
• เทคนิคการถ่ายภาพทางการแพทย์ใช้รูปวงรีเช่นกัน เทคโนโลยี MRI และ อัลตราซาวด์ มักใช้การประมาณปริมาตรของอวัยวะด้วยรูปวงรี ซึ่งเป็นวิธีที่มีประสิทธิภาพในการวัดโดยไม่ต้องใช้การสแกนสามมิติเต็มรูปแบบ

คุณจะพบเครื่องมืออื่นๆ อีกมากใน คลังเครื่องมือคณิตศาสตร์ ที่ออกแบบมาสำหรับนักเรียน ครู และผู้เชี่ยวชาญ