เครื่องมือคำนวณส่วนเบี่ยงเบนมาตรฐาน

ส่วนเบี่ยงเบนมาตรฐานเป็นหนึ่งในคำที่คุณอาจเคยได้ยินในโรงเรียน — อาจในชั้นคณิตศาสตร์หรือปรากฏในรายงานวิจัย แต่เบื้องหลังชื่อที่ดูน่ากลัวนั้นคือแนวคิดที่เข้าใจง่ายและเป็นหัวใจหลักของทุกอย่างตั้งแต่การค้นพบทางวิทยาศาสตร์ไปจนถึงกลยุทธ์ทางธุรกิจและพยากรณ์อากาศ สรุปสั้นๆ ก็คือ มันช่วยให้เราเข้าใจการกระจาย — ว่าข้อมูลเบี่ยงออกจากศูนย์กลางไกลแค่ไหน ไม่ว่าจะเป็นคะแนนทดสอบ ราคา หรือผลลัพธ์ของผู้ป่วย การรู้วิธีวัดความแตกต่างนี้ช่วยเพิ่มความชัดเจน บริบท และความมั่นใจในข้อมูลที่เราใช้ทุกวัน

ดู คณิตศาสตร์ เพื่อใช้เครื่องมือเพิ่มเติม

ส่วนเบี่ยงเบนมาตรฐานคืออะไร?

ส่วนเบี่ยงเบนมาตรฐานวัดความกระจัดกระจายของค่าต่างๆ ในชุดข้อมูล เปรียบเสมือนการตอบคำถามว่า “ตัวเลขเบี่ยงออกจากค่าเฉลี่ยมากแค่ไหน?”

สมมติว่าครูให้ทำข้อสอบและนักเรียนทุกคนได้คะแนน 80 เต็ม 100 ค่าเฉลี่ยคือ 80 และทุกคนมีค่าเท่ากัน — ดังนั้นส่วนเบี่ยงเบนมาตรฐานจึงเป็นศูนย์ ไม่มีความแปรปรวนเลย แต่ลองนึกอีกกลุ่มหนึ่งที่มีค่าเฉลี่ยเท่ากันคือ 80 แต่คะแนนจริงเป็น 60, 70, 90 และ 100 ถึงแม้ค่าเฉลี่ยยังเป็น 80 แต่คะแนนกระจายห่างออกไปมาก กลุ่มที่สองจึงมีส่วนเบี่ยงเบนมาตรฐานสูงกว่า

ส่วนเบี่ยงเบนมาตรฐานต่ำหมายความว่าค่าต่างๆ กระจุกตัวรอบค่าเฉลี่ยอย่างแน่นหนา ส่วนเบี่ยงเบนมาตรฐานสูงหมายถึงการกระจายกว้างขึ้น

ทำไมเราถึงให้ความสำคัญกับความแปรปรวนของข้อมูล?

ความแปรปรวนไม่ใช่แค่เสียงรบกวนทางสถิติ — มันบอกเล่าเรื่องราว การวัดความผันผวนช่วยให้เราเห็นแนวโน้ม ค่าที่เบี่ยงออก (outliers) และรูปแบบที่อาจซ่อนอยู่ ในด้านสุขภาพใช้ประเมินว่าการรักษามีผลสม่ำเสมอหรือไม่ ด้านภูมิอากาศช่วยติดตามการเปลี่ยนแปลงอุณหภูมิที่ผิดปกติ ครูใช้วิเคราะห์ผลการเรียนของนักเรียนในโรงเรียนต่างๆ วิศวกรใช้ควบคุมคุณภาพ หากไม่เข้าใจความแปรปรวน เราอาจตีความข้อมูลผิดไป

ลองใช้เครื่องมือที่เกี่ยวข้อง: เครื่องมือคำนวณค่าเฉลี่ย, เครื่องมือคำนวณความแปรปรวน หรือเครื่องมือคำนวณค่า Z-Score เพื่อสำรวจวิธีที่ข้อมูลเล่าเรื่อง

ส่วนเบี่ยงเบนมาตรฐานของประชากร

เมื่อคุณมีข้อมูลจากประชากรทั้งหมดที่กำลังศึกษาคุณสามารถคำนวณส่วนเบี่ยงเบนมาตรฐานของประชากรได้โดยตรง วิธีนี้ช่วยกำหนดระดับความแปรปรวนที่แท้จริงของชุดข้อมูลทั้งหมด เช่น เมื่อคุณมีข้อมูลจากบุคคลทั้งหมดในประชากร หรือจุดทั้งหมดในการสำรวจครอบคลุมทุกกลุ่ม

สูตรคำนวณส่วนเบี่ยงเบนมาตรฐานของประชากร:

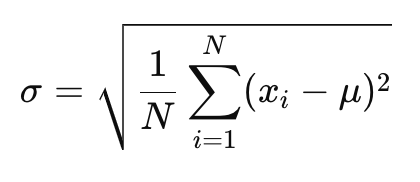
โดยที่:

𝜎: คือส่วนเบี่ยงเบนมาตรฐานของประชากร

𝑁: คือจำนวนการสังเกตในชุดข้อมูล (ขนาดประชากร)

x_i: คือค่าทุกค่าในชุดข้อมูล

𝜇: คือค่าเฉลี่ยของประชากร

ส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง

ใช้เมื่อคุณมีเพียงตัวอย่างข้อมูลที่แทนประชากรทั้งหมดไม่ได้ เนื่องจากไม่สามารถเก็บข้อมูลประชากรครบถ้วนได้ การคำนวณส่วนเบี่ยงเบนมาตรฐานของตัวอย่างจะมีการปรับแก้เพื่อชดเชยการประเมินเชิงอคติ ให้แน่ใจว่าการวัดจะไม่ประเมินค่าความกระจายต่ำกว่าความเป็นจริง

สูตรส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง: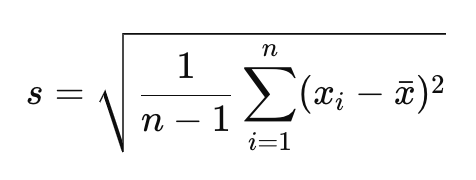

โดยที่:

𝑠: คือส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง

𝑛: คือจำนวนการสังเกตในตัวอย่าง

x̄: คือค่าเฉลี่ยของตัวอย่าง

กราฟระฆังคว่ำและการแจกแจงแบบปกติ

คุณคงเคยเห็นกราฟระฆังคว่ำ — เส้นโค้งรูปเนินที่ค่าส่วนใหญ่集中ที่ตรงกลางและน้อยกว่าที่ปลายข้างใดข้างหนึ่ง มันไม่ใช่แค่กราฟสวย แต่เป็นการแสดงการแจกแจงแบบปกติ ซึ่งพบในชีวิตจริงบ่อยครั้ง เช่น ส่วนสูง คะแนนไอคิว ผลสอบ หรือค่าความดันโลหิต

ตรงนี้เองที่ส่วนเบี่ยงเบนมาตรฐานเข้ามามีบทบาท มันกำหนดความกว้างหรือความแคบของระฆังคว่ำ หากค่าส่วนใหญ่ใกล้ค่าเฉลี่ย เส้นโค้งจะสูงและแคบ (ส่วนเบี่ยงเบนมาตรฐานเล็ก) แต่ถ้าค่ากระจายกว้าง เส้นโค้งจะกว้างและต่ำ (ส่วนเบี่ยงเบนมาตรฐานใหญ่)

มีกฎง่ายๆ ดังนี้:

• 68% ของค่าจะอยู่ภายใน 1 ส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย

• 95% ภายใน 2 ส่วนเบี่ยงเบนมาตรฐาน

• และ 99.7% ภายใน 3 ส่วนเบี่ยงเบนมาตรฐาน

ทำให้เข้าใจง่ายขึ้นว่า ค่าไหนถือว่าสมเหตุสมผล (หรือผิดปกติ) ไม่ว่าคุณจะวิเคราะห์คะแนนสอบหรือผลตอบแทนหุ้น

🎯 Fun Fact: การทดสอบ IQ ส่วนใหญ่ถูกออกแบบให้คะแนนตามกราฟระฆังคว่ำ — มีค่าเฉลี่ย 100 และส่วนเบี่ยงเบนมาตรฐาน 15 จึงทำให้คะแนน 130 ถูกจัดว่าเป็นกลุ่มอัจฉริยะ!