เครื่องคำนวณพื้นที่วงรี

จากวงโคจรดาวเคราะห์ไปจนถึงทรงโดมสถาปัตยกรรมที่ดูหรูหรา พื้นที่วงรีมีบทบาทสำคัญอย่างเงียบเชียบในการทำความเข้าใจและรังสรรค์สิ่งรอบตัวคุณ คุณอาจไม่จำเป็นต้องคำนวณมันทุกวัน แต่เมื่อไหร่ก็ตามที่ต้องใช้—ไม่ว่าจะเป็นโครงการออกแบบ วางผังภูมิทัศน์ หรือแก้ปัญหาทางเรขาคณิต คู่มือนี้จะพาคุณผ่าน เครื่องคำนวณพื้นที่วงรี ยกตัวอย่างประวัติศาสตร์ที่น่าสนใจ และอธิบายว่าทำไมรูปร่างไข่แบนนี้ถึงปรากฏในทุกอย่างตั้งแต่กีฬาจนถึงสถาปัตยกรรม หากคุณพร้อมจะวัดพื้นที่อย่างมีความงาม คุณมาถูกที่แล้ว

พื้นที่วงรีคืออะไร?

โดยสรุปคือปริมาณพื้นที่ที่ถูกล้อมรอบด้วยรูปไข่แบน ซึ่งเปรียบเสมือนวงกลมที่ยืดออก แตกต่างจากวงกลมสมบูรณ์ที่มีรัศมีเดียว การวัดวงรีใช้สองแกน ได้แก่แกนนอนที่ยาวกว่าและแกนดิ่งที่สั้นกว่า ซึ่งเรียกว่ากึ่งแกนเอกและกึ่งแกนโท โดยทั้งสองช่วยยืดรูปทรงให้เป็นเส้นโค้งเฉพาะตัว

วงรีไม่ได้อยู่แค่ในตำราทางทฤษฎี แต่พบเห็นได้ทั่วไป ในดาราศาสตร์ วงรีใช้กำหนดวงโคจรดาวเคราะห์ ในวิศวกรรม ช่วยกำหนดรูปทรงชิ้นส่วนและการกระจายแรง และในการออกแบบ วงรีปรากฏในเฟอร์นิเจอร์ กระจก ผังพื้น และแม้แต่โรงละครกลางแจ้ง

ตั้งแต่สนามวิ่งทรงวงรีที่นักกีฬาฝึกซ้อมไปจนถึงผังมหาวิหาร พื้นที่วงรีช่วยเติมเต็มทั้งรูปแบบและการใช้งานในโลกจริง

สำหรับรูปทรงอื่นๆ เช่น สี่เหลี่ยม วงกลม หรือรูปทรงไม่สม่ำเสมอ เครื่องมือคำนวณพื้นที่ รวบรวมตัวเลือกทั้งหมดไว้ในที่เดียว คุณสามารถสำรวจเครื่องมืออื่นๆ ได้ในหัวข้อเครื่องมือทางคณิตศาสตร์—ออกแบบมาเพื่อให้การคำนวณเรขาคณิต พีชคณิต และการวัดในชีวิตจริงเป็นเรื่องง่ายขึ้น

สูตรคำนวณพื้นที่วงรี

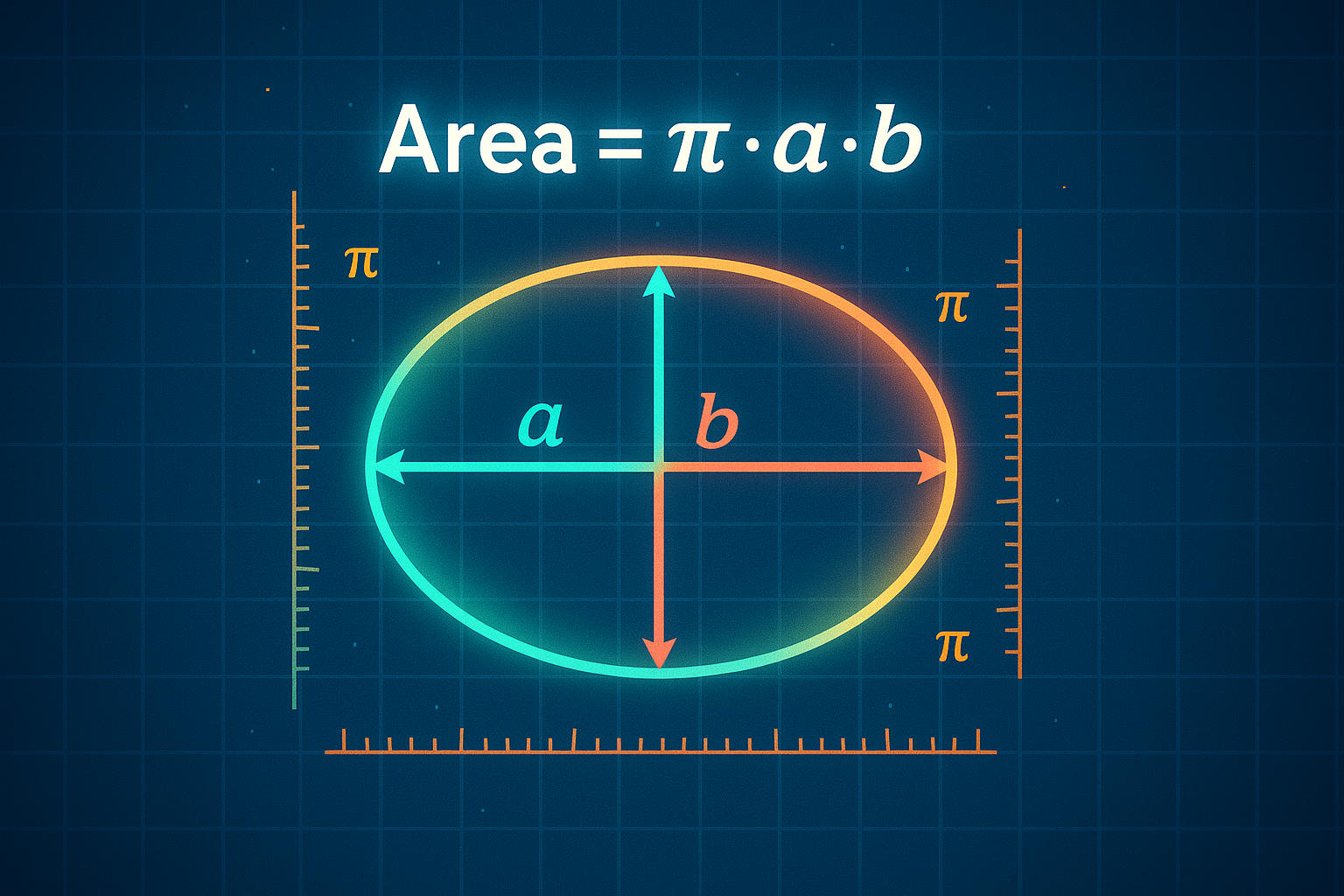
โชคดีที่การคำนวณพื้นที่ของวงรีไม่ซับซ้อนเท่าที่คิด สูตรคือ:

พื้นที่ = π × a × b

โดยที่:

• π (pi) ประมาณ 3.14159

• a คือกึ่งแกนเอก (ครึ่งหนึ่งของเส้นผ่านศูนย์กลางยาวสุดของวงรี)

• b คือกึ่งแกนโท (ครึ่งหนึ่งของเส้นผ่านศูนย์กลางสั้นสุดของวงรี)

ลองคิดแบบนี้: กึ่งแกนเอกบอกขนาดความกว้างของวงรี ส่วนกึ่งแกนโทบอกความสูง เมื่อคูณค่าทั้งสองเข้าด้วยกันแล้วคูณด้วย π ก็จะได้พื้นที่ที่แม่นยำและเรียบหรู

หากรูปทรงของคุณเป็นวงกลมแทนที่จะเป็นวงรี เครื่องคำนวณพื้นที่วงกลม จะให้ผลลัพธ์ที่รวดเร็วและแม่นยำ

The Whispering Gallery

หนึ่งในการใช้งานทางโลกจริงที่น่าทึ่งที่สุดของเรขาคณิตวงรีไม่ได้อยู่ในตำรา แต่ซ่อนอยู่ภายในมหาวิหารเซนต์พอลในลอนดอน ใต้โดมอันเป็นเอกลักษณ์มีทางเดินรูปวงกลมที่เรียกว่าThe Whispering Gallery—จุดที่เรขาคณิตกลายเป็นเสียง

นี่คือเรื่องน่าทึ่ง: ถ้าผู้เข้าชมสองคนยืนอยู่ตรงกันข้ามกันบนผนังโค้งที่ห่างกันกว่า 30 เมตร คนหนึ่งกระซิบที่ผนัง อีกคนจะได้ยินเสียงนั้นชัดเจนโดยไม่มีไมโครโฟนหรือเสียงก้อง เพียงแค่เสียงถูกสะท้อนและนำทางอย่างแม่นยำ

ทำไมมันถึงได้ผล? เพราะวิธีที่วงรีสะท้อนคลื่น ในวงรีใดๆ คลื่นเสียง (หรือแสง) ที่เริ่มจากจุดโฟกัสหนึ่ง จะสะท้อนจากผนังโค้งแล้วส่งตรงไปยังอีกจุดโฟกัสหลัก นั่นเองที่เหมือนหลักการเบื้องหลังสูตรพื้นที่วงรี แกนสองเส้นเล็กๆ กลับกำหนดได้มากกว่าพื้นที่ พวกมันยังเปลี่ยนทิศทางการเคลื่อนที่ของเสียงอีกด้วย

การเลือกสถาปัตยกรรมนี้ไม่ใช่เรื่องบังเอิญ นักออกแบบมหาวิหารเซนต์พอลใช้พลังของคณิตศาสตร์วงรีสร้างสรรค์งานสถาปัตยกรรมที่ไม่เพียงสวยงาม แต่ยังสร้างประสบการณ์อัศจรรย์ให้ผู้คนได้สัมผัสมาจนถึงทุกวันนี้