เครื่องมือคำนวณพื้นที่ภาคส่วน (ตารางฟุต)

จากการออกแบบสวนโค้งไปจนถึงการวางผังโรงละครกลางแจ้ง, พื้นที่ภาคส่วน เป็นแนวคิดสำคัญในการวางแผนพื้นที่วงกลม บทแนะนำนี้จะช่วยให้คุณเข้าใจพื้นฐานเรขาคณิตวงกลม สำรวจการใช้งานจริง และเปิดเผยข้อเท็จจริงน่าสนใจบางประการ—.

ถ้าต้องการเรียนรู้เกี่ยวกับรูปทรงอื่นๆ ลองใช้คอลเลกชั่น เครื่องมือคำนวณพื้นที่ตารางฟุต Calculators ของเรา

พื้นที่ภาคส่วนคืออะไร?

ภาคส่วน คือส่วนหนึ่งของวงกลม—เหมือนชิ้นพิซซ่า ส่วนในไพชาร์ต หรือส่วนหนึ่งของแปลงสวนทรงกลม นิยามโดย รัศมีสองเส้น และ ส่วนโค้ง ระหว่างเส้น เมื่อพูดถึง พื้นที่ภาคส่วน หมายถึงพื้นที่ของชิ้นส่วนดังกล่าว ซึ่งปกติวัดเป็น ตารางฟุต

เนื่องจากวงกลมเต็มมี 360 องศา ขนาดของภาคส่วนขึ้นอยู่กับทั้ง รัศมี ของวงกลมและ มุม ของภาคส่วนนั้น ตัวอย่างเช่น ภาคส่วนมุม 90° จะครอบคลุม หนึ่งในสี่ ของวงกลมทั้งหมด

คุณจะพบแนวคิดนี้ในหลายสถานการณ์ปฏิบัติ—เช่น การวางผัง น้ำพุทรงกลม การกำหนด ระยะเอื้อมของเรดาร์ หรือการคำนวณพื้นที่ที่ สปอร์ตไลต์ ส่องบนเวที

💡 Fun Fact: NASA ใช้สูตรคำนวณพื้นที่ภาคส่วนเมื่อวางแผนการครอบคลุมสัญญาณดาวเทียมบนโลก เนื่องจากดาวเทียมหลายดวงส่งสัญญาณในรูปแบบวงกลมหรือรัศมี การคำนวณพื้นที่ภาคส่วนช่วยวิศวกรเพิ่มประสิทธิภาพการวางตำแหน่งดาวเทียมและหลีกเลี่ยงการซ้อนทับของโซนการสื่อสาร

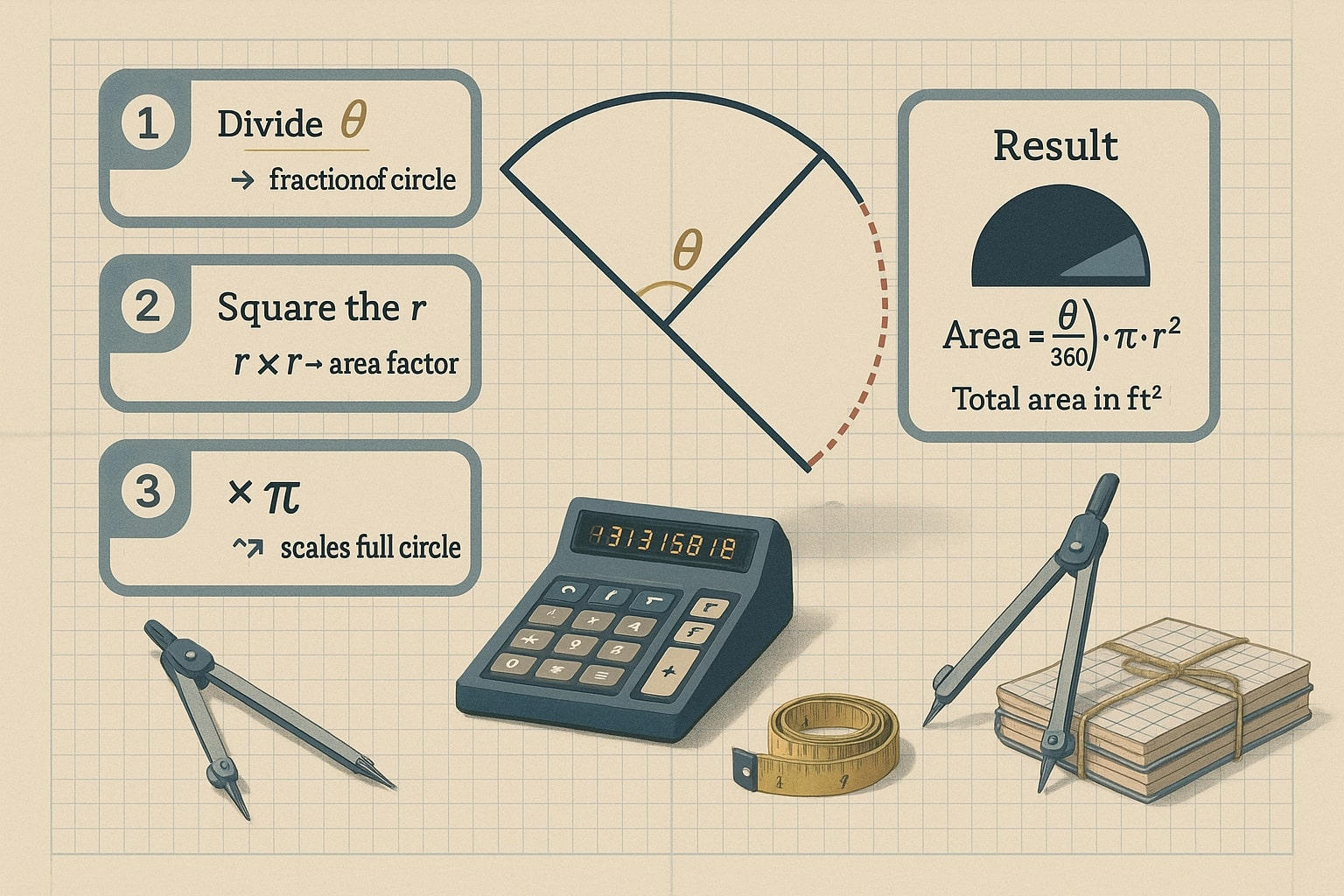
วิธีคำนวณพื้นที่ภาคส่วน (พร้อมตัวอย่าง)

การหาพื้นที่ภาคส่วนนั้นง่ายกว่าที่คิด เพียงใช้สูตรต่อไปนี้:

Area of a sector = (θ / 360) × π × r²

มาดูส่วนประกอบของสูตร:

• θ คือ มุมส่วนกลาง ของภาคส่วน (หน่วย: องศา)

• r คือ รัศมี ของวงกลม (ระยะจากจุดศูนย์กลางถึงขอบ)

• π เป็นค่าคงที่ ประมาณ 3.1416

สูตรนี้ทำงานโดยคำนวณว่าส่วนมุมที่คุณกำลังพิจารณาเป็นสัดส่วนเท่าไรของวงกลมทั้งหมด—เนื่องจากวงกลมเต็มมี 360 องศา การนำมุมไปหารด้วย 360 จึงได้สัดส่วนนั้น

ตัวอย่าง: สมมติว่าคุณกำลังปลูกกระถางดอกไม้ทรงกลมที่มี รัศมี 6 ฟุต และต้องการหาพื้นที่ของ ภาคส่วนมุม 120°

ขั้นตอนที่ 1: กำหนดค่าตัวแปร

• รัศมี (r) = 6 ฟุต

• มุม (θ) = 120°

ขั้นตอนที่ 2: ใช้สูตร
Area = (120 / 360) × π × (6²)
= (1/3) × π × 36
= π × 12
≈ 3.1416 × 12
≈ 37.7 ตารางฟุต

ดังนั้น ภาคส่วนนี้ครอบคลุมพื้นที่ประมาณ 37.7 ตารางฟุต ของสวนคุณ

สำหรับรูปทรงที่ซับซ้อนกว่า—เช่น การวางผังที่ผสมผสานภาคส่วน สี่เหลี่ยม และพื้นที่อื่นๆ—คุณสามารถใช้ เครื่องมือคำนวณพื้นที่ตารางฟุต เพื่อแยกคำนวณและให้ได้ผลรวมที่แม่นยำยิ่งขึ้น

สวนวงกลมในเกียวโต

ซ่อนตัวหลังผนังสงบเงียบของวัดเซนที่ไม่ค่อยมีคนรู้จักใน เกียวโต ประเทศญี่ปุ่น มีสวนที่โดดเด่นโดนเรียกโดยชาวบ้านว่า “En no Niwa” หรือ สวนวงกลม เมื่อแรกมองอาจดูเรียบง่าย: เส้นโค้งของหิน มอส และกรวดจัดวางอย่างประณีตราวกับคลื่นที่กระจายออกจากจุดศูนย์กลาง แต่เบื้องหลังงานออกแบบอันสงบนั้นคือการประยุกต์ใช้เรขาคณิตวงกลมที่ลึกซึ้งยาวนานหลายศตวรรษ

สวนนี้ได้รับแรงบันดาลใจจาก เอนโสะ สัญลักษณ์วงกลมของเซนพุทธซึ่งแทนถึงปัญญา ความสมบูรณ์ และกระบวนการหมุนเวียนของชีวิต เมื่อสวนนี้ถูกออกแบบใหม่ในปลายศตวรรษที่ 1600s บันทึกของวัดแสดงให้เห็นว่าสามเณรร่วมมือกับช่างสวนผู้ชำนาญที่ใช้ภาพร่างภาคส่วนวาดมือเพื่อกำหนดความกว้างของส่วนโค้งแต่ละส่วน พวกเขาคำนวณมุมและรัศมีเพื่อให้แต่ละจุดของมอสหรือกรวดคลุมพื้นที่ที่พอดี สร้างจังหวะและความกลมกลืนที่ดีที่สุดเมื่อชมจาก แท่นภาวนาของวัด

แน่นอน พวกเขาไม่ได้ใช้คำว่า “sector square footage” แต่แนวคิดเหมือนกัน โดยการวัด มุม และ รัศมี ให้แม่นยำ พวกเขาจึงสามารถจัดวางมอสหรือกรวดได้ในปริมาณที่เหมาะสม สร้างความสมดุลและบรรยากาศสงบเงียบที่ดีที่สุดสำหรับการชม

ไปที่ส่วน คณิตศาสตร์ เพื่อแก้โจทย์คณิตได้อย่างรวดเร็วและง่ายดาย