เครื่องมือคำนวณเลขผสมเศษส่วน

เลขผสม — เช่น 2 ½ หรือ 5 ¾ — ไม่ใช่แค่ปัญหาคณิตศาสตร์ในโรงเรียนเท่านั้น แต่ยังใช้เขียนสูตรอาหาร ขายไม้ และวัดระยะทางในกีฬาอีกด้วย

เลขผสมกับเศษส่วนไม่เต็ม (เศษส่วนไม่สุภาพ)

ถ้าคุณเคยตวงแป้ง 2 ½ ถ้วย หรือได้ยินใครพูดว่าวิ่งไป 5 ¾ ไมล์ แสดงว่าคุณได้ใช้เลขผสม ตัวเลขผสมคือการรวมตัวเลขจำนวนเต็มกับเศษส่วนแท้ เช่น 3 ½ คือสามจำนวนเต็มบวกกับเศษครึ่งหนึ่ง เลขผสมเป็นที่คุ้นเคย ใช้งานง่าย และพบได้บ่อยในชีวิตประจำวันกว่าที่เราคิด

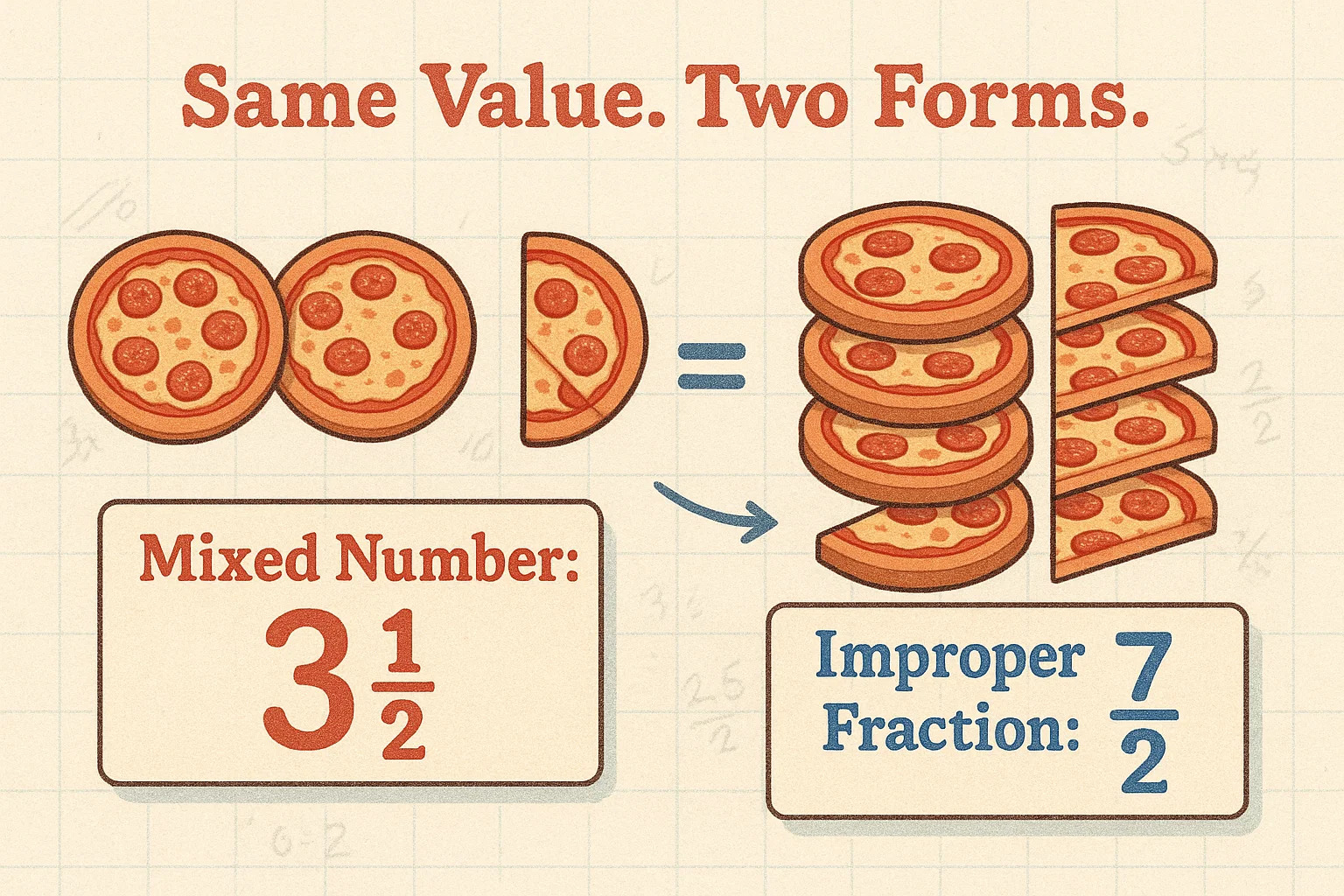
ในทางตรงกันข้าม เศษส่วนไม่เต็มอาจดูซับซ้อนกว่าแต่ใช้คณิตศาสตร์เหมือนกัน โดยเศษส่วนไม่เต็มคือเศษส่วนที่ตัวเศษ (ตัวบน) เท่ากับหรือมากกว่าตัวส่วน (ตัวล่าง) เช่น ⁷⁄₂ ซึ่งมีค่าเท่ากับ 3 ½ เพียงแต่เขียนในรูปแบบต่างกัน

ทำไมเราถึงใช้สองรูปแบบนี้สำหรับค่าที่เท่ากัน? เลขผสมเข้าใจง่ายในทันที ขณะที่เศษส่วนไม่เต็มเหมาะกับการคำนวณจริง โดยเฉพาะในพีชคณิตหรือการเขียนโปรแกรม

วิธีแปลงเลขผสมเป็นเศษส่วนไม่เต็ม:

สมมติว่าคุณมี 4 ⅗

1. คูณจำนวนเต็มกับตัวส่วน: 4 × 5 = 20
2. บวกตัวเศษ: 20 + 3 = 23
3. เขียนไว้เหนือจำนวนเต็มเดิม: ²³⁄₅

ดังนั้น 4 ⅗ จะกลายเป็น ²³⁄₅

นี่เป็นขั้นตอนทั่วไปเมื่อต้องแปลงเลขผสมเป็นเศษส่วนไม่เต็มก่อนนำไปคูณหรือหาร

วิธีแปลงเศษส่วนไม่เต็มกลับเป็นเลขผสม:

สมมติ ¹¹⁄₄

1. หารตัวเศษด้วยตัวส่วน: 11 ÷ 4 = 2 เศษ 3
2. จำนวนเต็มคือ 2 ส่วนเศษที่เหลือคือ 3 ซึ่งจะเป็นตัวเศษใหม่
3. ตัวส่วนยังคงเดิม: 2 ¾

นี่คือวิธีแปลงเมื่อเริ่มต้นจากเศษส่วนไม่เต็มให้เป็นเลขผสม

เรื่องน่ารู้: “ในภารกิจ Apollo 13 วิศวกร NASA ใช้ไม้บรรทัดเลื่อนและการคำนวณมือกับเศษส่วนเช่น 2 ⁵⁄₈ เพื่อเปลี่ยนเส้นทางยานอย่างรวดเร็วและช่วยชีวิตทีมงาน” — เอกสาร NASA¹

วิธีคำนวณเลขผสมเศษส่วน

เมื่อต้องบวก ลบ คูณ หรือหารเลขผสม จะต้องจัดการกับจำนวนเต็มและเศษส่วนให้ลงตัว เคล็ดลับคือทำคณิตศาสตร์ให้เรียบง่ายและสะอาดเสมอ — และอย่าลืมย่อเศษส่วนให้เรียบร้อยหลังจากคำนวณเสร็จ ไม่ว่าจะเพิ่มสูตรอาหารเป็นสองเท่าหรือทำโจทย์สอบ กฎง่ายๆ เหล่านี้จะช่วยให้คุณทำได้รวดเร็วและแม่นยำ

การบวกและลบ

เริ่มด้วยแยกจำนวนเต็มกับส่วนเศษออกจากกัน เลขผสมมีสองส่วนนี้ ดังนั้นทำคำนวณกับแต่ละส่วนก่อน แล้วค่อยรวมผลลัพธ์เข้าด้วยกัน

ลองดูตัวอย่าง:

บวก: 2 ½ + 3 ¾

1. บวกจำนวนเต็ม: 2 + 3 = 5
2. บวกเศษส่วน: ½ + ¾ → แปลงหารร่วม → ²⁄₄ + ³⁄₄ = ⁵⁄₄
3. ตอนนี้ได้: 5 + ⁵⁄₄ → แต่ ⁵⁄₄ = 1 ¼ ดังนั้นคำตอบสุดท้ายคือ:
   → 6 ¼

ลบ: 5 ⅚ − 2 ⅔

1. จำนวนเต็ม: 5 - 2 = 3
2. เศษส่วน: ⁵⁄₆ − ²⁄₃ → แปลง ²⁄₃ = ⁴⁄₆ → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆
3. คำตอบสุดท้าย: 3 ¹⁄₆

เมื่อการลบทำให้เศษส่วนติดลบ (เช่น ¼ − ¾) อาจต้องยืมจากจำนวนเต็ม อย่าข้ามขั้นตอนนี้เพราะเป็นสาเหตุหลักของความผิดพลาด หรือจะใช้เครื่องมือย่อเศษส่วนตรวจสอบคำตอบอีกครั้ง

การคูณ

การคูณเลขผสมเริ่มจากการแปลงเป็นเศษส่วนไม่เต็มก่อน

สมมติคุณทำการคูณ: 2 ⅓ × 1 ½

1. แปลงเป็นเศษส่วนไม่เต็ม:
   2 ⅓ = ⁷⁄₃
   1 ½ = ³⁄₂
2. คูณข้าม:
   ⁷⁄₃ × ³⁄₂ = ²¹⁄₆
3. ย่อเศษส่วน:
   ²¹⁄₆ = 3 ½

ตอนนี้คุณพร้อมแล้ว

ข้อมูลเสริม: “งานวิจัยในโรงเรียนมัธยมที่ชิคาโกพบว่านักเรียนที่ฝึกแปลงเลขผสมก่อนการคูณ คะแนนสอบดีขึ้น 27% เมื่อเทียบกับผู้ที่เดาจากภาพ” — การศึกษากระทรวงศึกษาธิการสหรัฐฯ²

การคูณทำได้ง่ายเพราะทำงานกับตัวเลขทั้งหมดโดยไม่ต้องเปลี่ยนหารเหมือนกับการบวกหรือลบ หากไม่แน่ใจในการคูณ ลองคำนวณด้วยมือก่อนแล้วใช้เครื่องมือคำนวณเศษส่วนตรวจสอบผลลัพธ์

การหาร

การหารมักถูกมองว่ายาก แต่จริงๆ แล้วเป็นการคูณโดยสลับเศษส่วน

ตัวอย่าง: หาร 3 ¾ ÷ 1 ½

1. แปลงเป็นเศษส่วนไม่เต็ม:
   3 ¾ = ¹⁵⁄₄
   1 ½ = ³⁄₂
2. กลับเศษส่วนที่สอง (ตัวหาร):
   ³⁄₂ กลายเป็น ²⁄₃
3. คูณ:
   ¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂
4. ย่อเศษส่วน:
   ³⁰⁄₁₂ = 2 ½

เท่านี้แหละ — แค่กลับและคูณ

หากคำตอบอยู่ในรูปเศษส่วนไม่เต็ม เช่น ²¹⁄₄ คุณสามารถเก็บไว้อย่างนั้นสำหรับพีชคณิตหรือการเขียนอย่างเป็นทางการ หรือนำมาแปลงเป็นเลขผม (5 ¼) สำหรับใช้ในชีวิตประจำวัน

ไม่ว่าจะในห้องเรียนหรือห้องครัว การรู้วิธีจัดการกับการคำนวณเหล่านี้จะช่วยให้คุณทำคณิตศาสตร์ได้ทุกสถานการณ์ — แม้ตัวเลขจะดูซับซ้อนขนาดไหน และถ้ายังไม่มั่นใจสามารถตรวจสอบขั้นตอนด้วยเครื่องมือคำนวณคณิตศาสตร์ได้

เมื่อเศษส่วนช่วยงานก่อสร้างไม่ให้ล่าช้า

เลขผสมไม่ใช่แค่เรื่องในห้องเรียน บางครั้งยังช่วยประหยัดเวลา เงิน และโครงการทั้งโครงการ

หัวหน้าทีมก่อสร้างในเมืองเดสมอยน์ รัฐไอโอวา แชร์เรื่องราวที่การอ่านขนาดผิดเพียงครั้งเดียวเกือบทำให้โครงการปรับปรุงโรงเรียนล่าช้าแบบไม่ทันตั้งตัว แบบแปลนระบุขนาดแต่งโลหะพิเศษที่ 8 ⅜ นิ้ว ช่างฝึกงานใหม่ไม่คุ้นเคยกับการแปลงเศษส่วน อ่านผิดเป็น 8.3 นิ้ว ผลลัพธ์คือแผ่นอลูมิเนียมสั้นเกินไปเกือบ ¹⁄₁₆ นิ้ว ซึ่งเพียงพอที่จะไม่ผ่านการตรวจสอบ

ความผิดพลาดนี้ทำให้ทีมเสียเวลาทำงานซ้ำอีกหนึ่งสัปดาห์และวัสดุมูลค่ามากกว่า 4,000 ดอลลาร์สหรัฐ

“ฉันเรียนรู้จากความผิดพลาด — ทศนิยมไม่ได้ช่วยเสมอไป เลขผสมต่างหากคือสิ่งที่เทปลูกหน่วยวัดใช้จริง มันคือ ⅜ ไม่ใช่ 0.375 ความไม่ต่างนี้อาจทำให้เงินเดือนคุณหายได้” — ทิม เวกา หัวหน้าทีมก่อสร้างบริษัท Vega & Sons Build Co.⁴

ตอนนี้ก่อนส่งขนาดไปที่ร้านผลิต ทีมจะตรวจสอบกับตารางแปลงเศษส่วนเป็นทศนิยมที่พิมพ์และแปะไว้ที่กล่องเครื่องมือทุกกล่อง — และพนักงานใหม่จะได้เรียนรู้การบวกและลบเลขผสมด้วยตัวส่วนที่เหมือนกันอย่างรวดเร็ว

เลขผสมไม่ใช่เรื่องเพ้อฝันทางวิชาการ แต่ปรากฏอยู่ในแบบแปลน สูตรอาหาร ใบแจ้งหนี้ สถิติกีฬา และแม้แต่การปรับเทียบเครื่องมือ การเข้าใจการทำงานของเลขผสมช่วยให้คุณรับมือกับโลกจริงได้อย่างมั่นใจพร้อมเทปลูกหน่วยวัดในมือ

1. NASA. “ตีตารางภารกิจ Apollo 13.”
2. กระทรวงศึกษาธิการสหรัฐฯ “งานวิจัยคณิตศาสตร์โรงเรียนมัธยม”
3. โครงการอบขนมและทำอาหาร Napa Valley College, สัมภาษณ์เรื่องเล่า, มีนาคม 2023
4. สัมภาษณ์ทิม เวกา, มิถุนายน 2022. มาตรฐานและตรวจสอบการก่อสร้าง, กระทรวงความปลอดภัยสาธารณะรัฐไอโอวา