เครื่องมือคำนวณรูทที่สามของจำนวน

เครื่องมือคำนวณรูทที่สามของจำนวน เป็นเครื่องมือสำคัญสำหรับผู้ที่ต้องการหาค่ารูทที่สาม (หรือรากที่ 3) ของจำนวนบวก เครื่องมืออเนกประสงค์นี้ไม่เพียงช่วยให้งานหาค่ารูทที่สามทำได้ง่ายขึ้น แต่ยังช่วยให้ผู้ใช้หาค่ากำลังสามของตัวเลขได้อย่างสะดวก ไม่ว่าคุณจะกำลังแก้โจทย์คณิตศาสตร์ หาจำนวนลูกบาศก์สมบูรณ์ หรือคำนวณรูทของกำลังอื่น ๆ เครื่องมือนี้ก็ช่วยให้ผลลัพธ์แม่นยำและรวดเร็ว
รูทที่สามของจำนวนคืออะไร?
รูทที่สาม ของจำนวน คือค่าที่เมื่อนำมาคูณกับตัวเองจำนวน สามครั้ง จะได้ผลลัพธ์เป็นจำนวนดั้งเดิม ทางคณิตศาสตร์เขียนได้เป็น: ³√x = y ซึ่งหมายถึงว่า y³ = x
หรืออีกวิธีคือ: ³√x = x^{1/3}
ลองอธิบายง่าย ๆ: ถ้าคุณต้องหารูทที่สามของ 27 ก็คือการหาจำนวนที่เมื่อคูณด้วยตัวเองสามครั้งแล้วได้ 27 คำตอบคือ 3 เพราะ 3 × 3 × 3 = 27 แนวคิดนี้เป็นพื้นฐานสำคัญใน เลขคณิตและพีชคณิต รวมถึงการศึกษาเชิงคณิตศาสตร์ขั้นสูงอื่น ๆ
ความสัมพันธ์ทางเรขาคณิตของรูทที่สาม
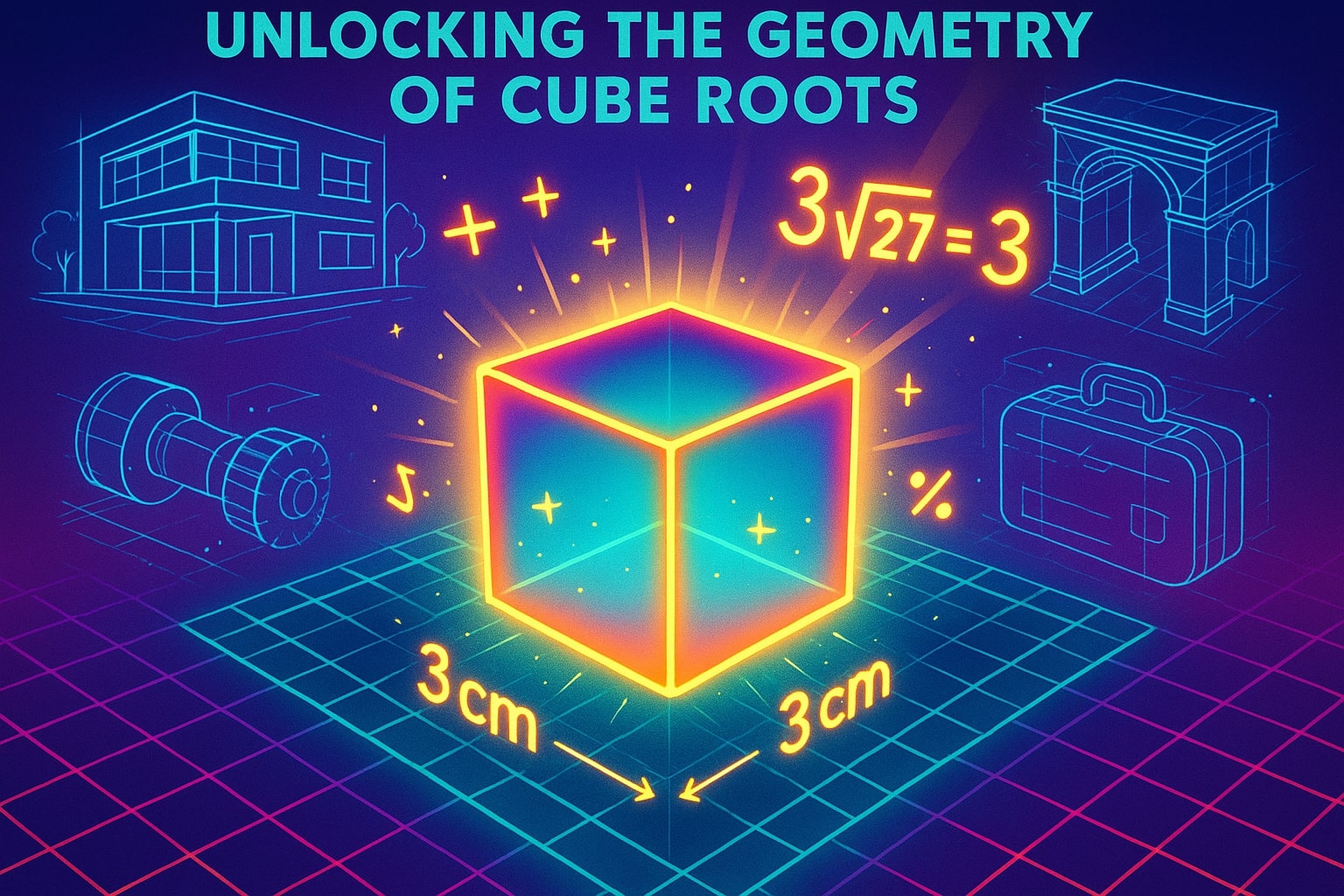
แนวคิดนี้ยังสามารถเชื่อมโยงกับรูปทรงสามมิติได้ ลองนึกภาพลูกบาศก์ที่มีปริมาตร 27 ลูกบาศก์เซนติเมตร ถ้าต้องการหาความยาวด้านหนึ่ง คุณจะคำนวณรูทที่สามของ 27 จะได้ความยาวด้านละ 3 เซนติเมตร เพราะ 3³ = 27
ความเชื่อมโยงนี้ทำให้รูทที่สามมีความสำคัญมากในด้าน เรขาคณิต วิศวกรรม สถาปัตยกรรม และ การออกแบบผลิตภัณฑ์ ที่ต้องเข้าใจพื้นที่สามมิติ
สำหรับการคำนวณในงานออกแบบสองมิติ ดูได้จาก เครื่องมือคำนวณพื้นที่สี่เหลี่ยมจัตุรัส
จำนวนลูกบาศก์สมบูรณ์คืออะไร?
จำนวนลูกบาศก์สมบูรณ์ คือผลลัพธ์ของการนำจำนวนเต็มมายกกำลังสาม การรู้จักจำนวนเหล่านี้ช่วยให้การแก้ปัญหาทำได้เร็วขึ้น นี่คือตัวอย่างจำนวนที่ใช้บ่อย:
ค่าพวกนี้ถูกใช้บ่อยในเรขาคณิต ฟิสิกส์ และคณิตศาสตร์เพื่อความรวดเร็วในการอ้างอิงและแก้ปัญหา การรู้จักจำนวนลูกบาศก์สมบูรณ์มีประโยชน์มากเวลาใช้คำนวณรูทที่สามหรือตรวจสอบว่าจำนวนใดแสดงออกมาได้ในรูปกำลังสามของจำนวนเต็มหรือไม่
| จำนวน | จำนวนลูกบาศก์สมบูรณ์ |
|---|---|
| 1³ | 1 |
| 2³ | 8 |
| 3³ | 27 |
| 4³ | 64 |
| 5³ | 125 |
| 6³ | 216 |
| 7³ | 343 |
| 8³ | 512 |
| 9³ | 729 |
| 10³ | 1,000 |
ฟังก์ชันรูทที่สามและกราฟ
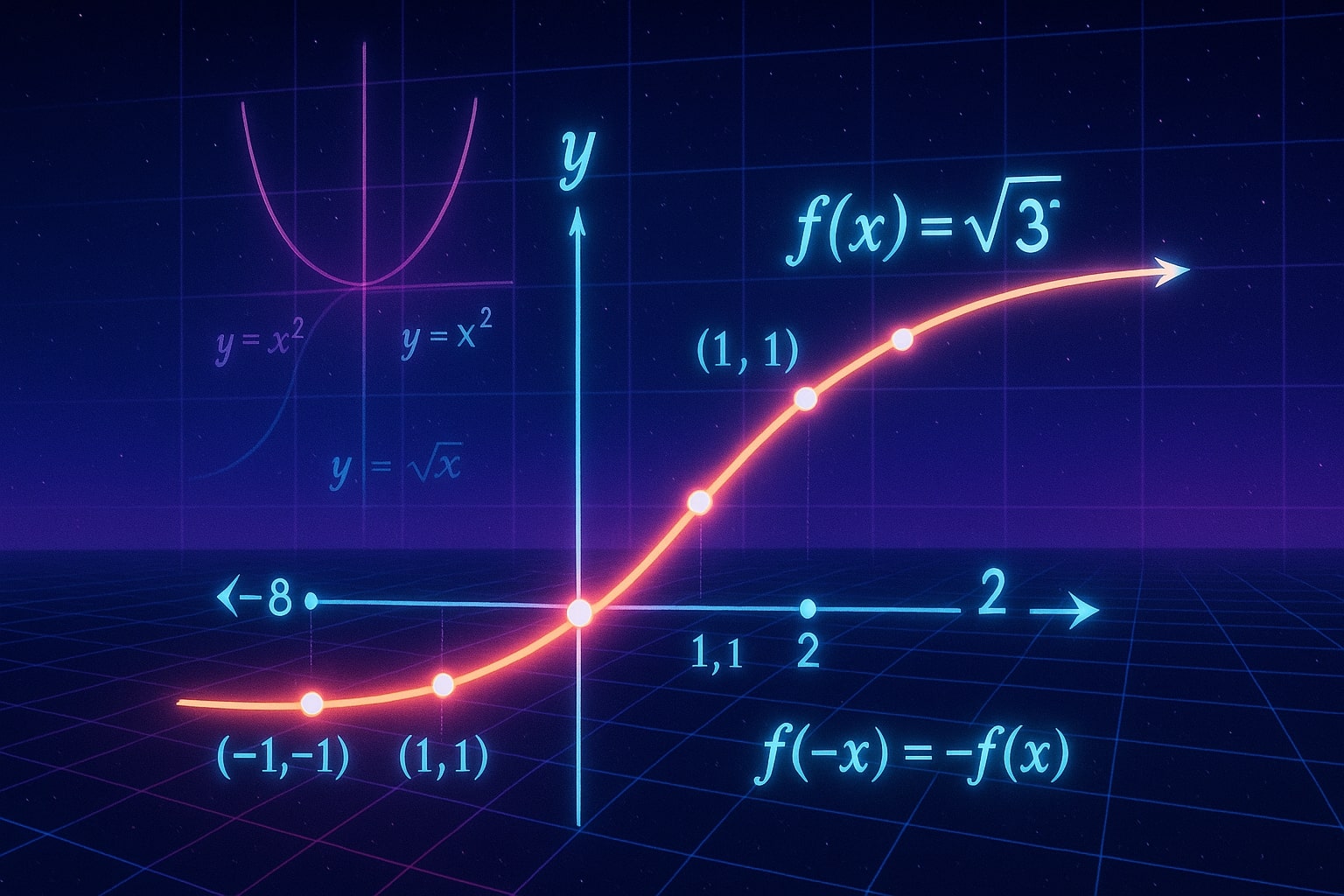
ฟังก์ชันรูทที่สาม ซึ่งเขียนเป็น f(x) = ³√x เป็นฟังก์ชันลักษณะ ฟังก์ชันคี่ หมายความว่ากราฟมี สมมาตรรอบจุดกำเนิด สมบัตินี้แสดงด้วย:
f(−x) = −f(x)
ลักษณะเด่นของฟังก์ชันรูทที่สาม:
- ผ่านจุดกำเนิด: กราฟจะตัดที่จุด (0, 0) อย่างเป็นธรรมชาติ
- ขอบเขตค่าบนแกน x และ y: ครอบคลุมจำนวนจริงทั้งหมด (ℝ)
- พฤติกรรม: เมื่อ x เข้าใกล้อินฟินิตี้บวก ค่า y จะเพิ่มขึ้น และเมื่อ x เข้าใกล้อินฟินิตี้ลบ ค่า y จะลดลง
กราฟของ ³√x = y มีลักษณะโค้งเรียบ เพิ่มหรือลดอย่างช้า ๆ ทำให้แตกต่างจากกราฟพาราโบลา (กำลังสอง) หรือกราฟรูทที่สองที่มีการเปลี่ยนแปลงที่ชัดเจนกว่ามาก
สำหรับการเปรียบเทียบกับฟังก์ชันรูทที่สอง ลองใช้ เครื่องมือคำนวณรูทที่สอง
สำหรับเครื่องมืออื่น ๆ ในกลุ่มนี้ สามารถเข้าใช้งานได้ที่ชุดเครื่องมือ เครื่องมือคำนวณทางคณิตศาสตร์ ของเรา
