เครื่องมือคำนวณสามเหลี่ยมมุมฉาก

สามเหลี่ยมมุมฉากคืออะไร

สามเหลี่ยมมุมฉากคือสามเหลี่ยมที่มีมุมหนึ่งเท่ากับ 90° พอดี มุมฉากนี้สร้างด้านสองด้านที่เรียกว่า ขา ซึ่งมาต่อกันที่มุม และด้านยาวอีกด้านหนึ่งที่ตรงข้ามมุมฉาก เรียกว่าด้านตรงข้ามมุมฉาก (hypotenuse) โดยในสูตรส่วนใหญ่ ขาสองด้านจะเรียกว่า a และ b ส่วนด้านตรงข้ามมุมฉากจะเรียกว่า c

สามเหลี่ยมมุมฉากมักพบได้แทบทุกที่—ตั้งแต่ความลาดเอียงของหลังคา คานรับแรงในสะพาน หรือแม้แต่เงาที่เกิดจากเสาไฟถนน ในทางคณิตศาสตร์ พวกมันเป็นที่ชื่นชอบเพราะช่วยให้แก้สมการหาค่าที่ขาดหายไปได้ง่ายเพียงแค่ใช้ตัวเลขไม่กี่ตัว

ความโดดเด่นของสามเหลี่ยมมุมฉากอยู่ที่ความสัมพันธ์ในตัวเองระหว่างสามด้าน ขอบคุณทฤษฎีบทของปีทาโกรัส (Pythagorean theorem) ถ้ารู้ด้านใดสองด้าน จะหาด้านที่เหลืออีกด้านได้เสมอ นั่นคือเหตุผลที่สามเหลี่ยมมุมฉากเป็นพื้นฐานของเรขาคณิต ทฤษฎีตรีโกณมิติ และฟิสิกส์

วิธีคำนวณสามเหลี่ยมมุมฉาก

สามเหลี่ยมมุมฉากทุกตัวเป็นไปตามกฎง่ายๆ คือ: a² + b² = c²

นี่คือทฤษฎีบทของปีทาโกรัสซึ่งเชื่อมโยงขาสองด้าน (a และ b) กับด้านตรงข้ามมุมฉาก (c) หากรู้ขาสองด้านใดก็ได้ สามารถหาด้านที่ขาดหายไปได้เสมอ

เช่น ถ้าขาทั้งสองยาว 3 และ 4 หน่วย ด้านตรงข้ามมุมฉากจะเท่ากับ:

c = √(3² + 4²) = √(9 + 16) = 5

สามเหลี่ยมมุมฉาก 3–4–5 เป็นตัวอย่างคลาสสิกเพราะเลขง่าย แต่กฎนี้ใช้ได้กับสามเหลี่ยมมุมฉากทุกรูปแบบ—แม้แต่เลขทศนิยมหรือค่ามากๆ

คุณยังสามารถจัดรูปแบบสมการใหม่เพื่อหาขาที่หายไปได้:

• a = √(c² − b²)

• b = √(c² − a²)

สูตรเหล่านี้ช่วยให้การคำนวณเป็นเรื่องง่าย ทั้งเวลาทำด้วยมือหรือเมื่อต้องตรวจสอบคำตอบอีกครั้ง

การหามุมในสามเหลี่ยมมุมฉาก

เมื่อรู้ความยาวด้านของสามเหลี่ยมมุมฉากแล้ว การหามุมเป็นเรื่องตรงไปตรงมาด้วยตรีโกณมิติ สัดส่วนที่ใช้กันบ่อยมาจากอัตราส่วนตามธรรมชาติของสามเหลี่ยม:

• ใช้สัมผัส: θ = arctan(a⁄b) — เหมาะสำหรับกรณีที่รู้ความยาวขาทั้งสอง

• ใช้ไซน์: θ = arcsin(a⁄c) — ใช้เมื่อรู้ความยาวขาและด้านตรงข้ามมุมฉาก

ฟังก์ชันเหล่านี้ช่วยค้นหามุมที่ขาดหายไปได้อย่างง่ายดาย เมื่อรู้มุมแหลมมุมหนึ่งแล้ว มุมอีกมุมจะเท่ากับ 90° − θ

สำหรับผู้ที่อยากตรวจสอบหรือศึกษาลึกลงไป สามารถใช้เครื่องมือที่เกี่ยวข้อง เช่น เครื่องมือคำนวณตรีโกณมิติ เพื่อช่วยตรวจสอบมุมเหล่านี้อย่างรวดเร็ว

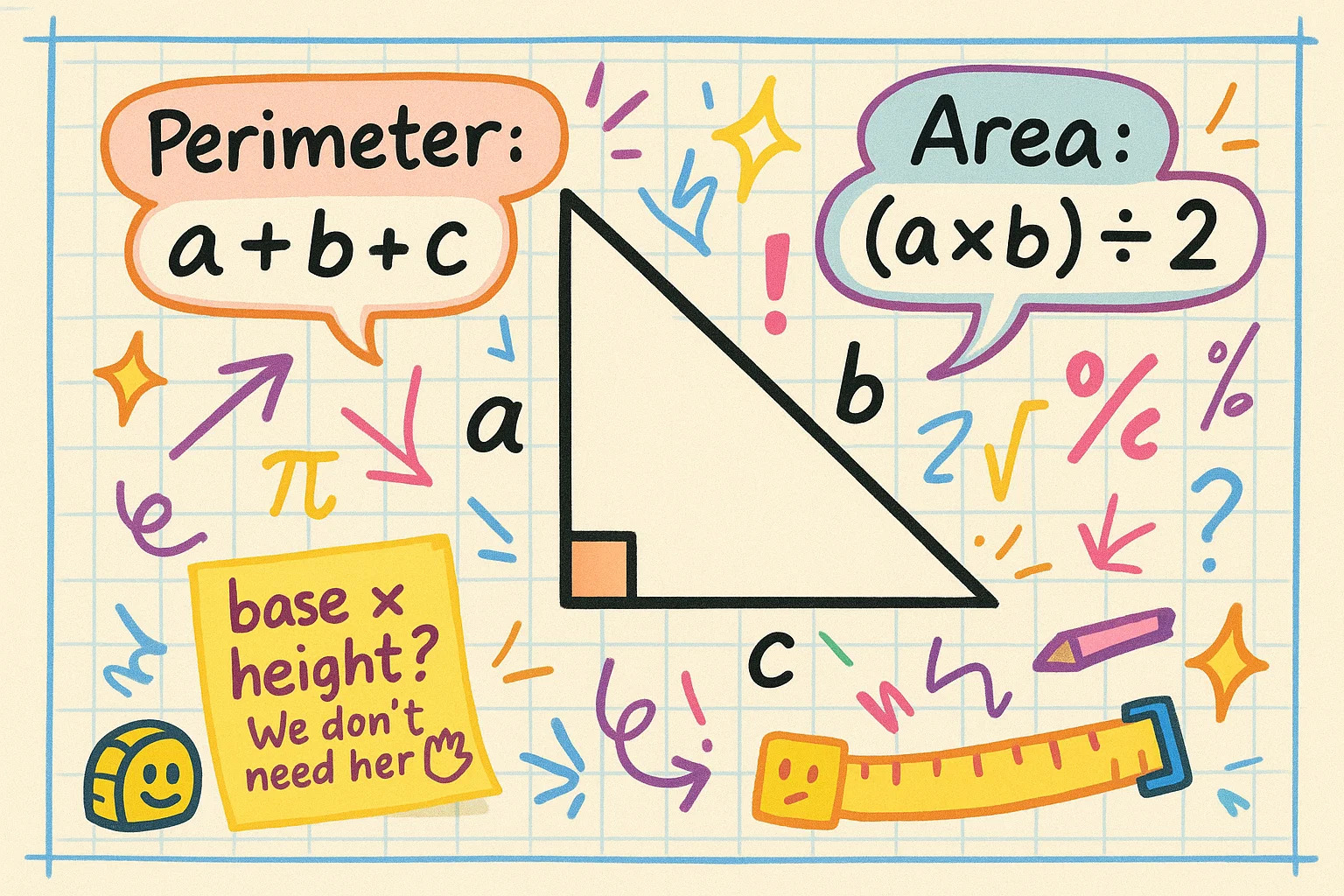
เส้นรอบรูปและพื้นที่ของสามเหลี่ยมมุมฉาก

เมื่อรู้ด้านของสามเหลี่ยมมุมฉาก การคำนวณเส้นรอบรูปและพื้นที่เป็นเรื่องง่าย เส้นรอบรูปคือการบวกความยาวทั้งสามด้าน: P = a + b + c

ส่วนพื้นที่มีสูตรลัดที่ใช้ได้กับสามเหลี่ยมมุมฉากทุกตัว: A = (a × b) ÷ 2

เพราะขาทั้งสองตั้งฉากกัน จึงทำหน้าที่เป็นฐานและความสูงโดยไม่ต้องใช้สูตรซับซ้อนหรือเส้นสูงพิเศษอื่นๆ

เช่น ถ้าสามเหลี่ยมมีขายาว 6 และ 8 หน่วย ด้านตรงข้ามมุมฉาก c เท่ากับ 10 (ตามทฤษฎีบทปีทาโกรัส) เส้นรอบรูปคือ 6 + 8 + 10 = 24 และพื้นที่คือ (6 × 8) ÷ 2 = 24

สูตรเหล่านี้ช่วยให้ประเมินขนาดสามเหลี่ยมได้รวดเร็วไม่ว่าจะเป็นงานบ้าน งานก่อสร้าง หรือโปรเจกต์ DIY

อัตราส่วนสามเหลี่ยมมุมฉากทั่วไป

สามเหลี่ยมมุมฉากบางประเภทปรากฏบ่อยในคณิตศาสตร์และชีวิตจริงจนควรจดจำ สามเหลี่ยม "พิเศษ" เหล่านี้มีอัตราส่วนของด้านคงที่ ทำให้ข้ามขั้นตอนคำนวณและหาด้านหรือมุมที่ขาดหายไปได้อย่างรวดเร็ว

สองประเภทที่พบบ่อยที่สุดคือ:

1. สามเหลี่ยม 30°–60°–90°

• ด้านมีอัตราส่วนคงที่เป็น 1 : √3 : 2

• ด้านสั้นที่สุด (ตรงข้ามมุม 30°) ใช้เป็นตัวอ้างอิง — ด้านตรงข้ามมุมฉากเป็นสองเท่าของด้านนี้ และขาที่ยาวกว่าคูณด้วย √3

• สองขามีความยาวเท่ากัน และด้านตรงข้ามมุมฉากจะเป็นขาคูณด้วย √2 เสมอ

• อัตราส่วนคือ 1 : 1 : √2

ตารางอ้างอิงอย่างรวดเร็ว:

การจดจำรูปแบบเหล่านี้ช่วยประหยัดเวลา โดยเฉพาะในการแก้โจทย์เรขาคณิตหรือตรีโกณมิติ

อยากฝึกโจทย์สามเหลี่ยมเพิ่มเติมไหม? ลองใช้ เครื่องมือคำนวณทางคณิตศาสตร์ เครื่องมือคำนวณทฤษฎีบทปีทาโกรัส และ เครื่องมือคำนวณตรีโกณมิติ ดูสิ